 ƒ(x) dx = F(x)
+ C, where C is a constant.
ƒ(x) dx = F(x)
+ C, where C is a constant.


Indefinite Integrals
Definition: A function F(x) is the antiderivative of a function ƒ(x) if for all x in the domain of ƒ,
 ƒ(x) dx = F(x)
+ C, where C is a constant.
ƒ(x) dx = F(x)
+ C, where C is a constant.Basic Integration Formulas
General and Logarithmic Integrals
| 1. kƒ(x) dx = k ƒ(x) dx | 2. 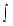 [ƒ(x) [ƒ(x)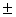 g(x)] dx = ƒ(x) dx g(x)] dx = ƒ(x) dx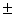 g(x) dx g(x) dx
|
3. 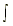 k dx = kx + C k dx = kx + C
| 4. 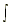 xn dx = xn dx = 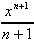 + C, n + C, n -1 -1
|
5. 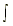 ex dx = ex + C ex dx = ex + C
| 6. 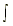 ax dx = ax dx = 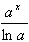 + C, a 0, a + C, a 0, a 1 1
|
7. 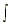 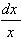 = ln |x| + C = ln |x| + C
|
Trigonometric Integrals
1. 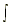 sin x dx = -cos x + C sin x dx = -cos x + C
| 2. 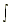 cos x dx = sin x + C cos x dx = sin x + C
|
3. 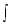 sec2 x dx = tan x + C sec2 x dx = tan x + C
| 4. 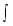 csc2 x dx = -cot x + C csc2 x dx = -cot x + C
|
5. 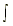 sec x tan x dx = sec x + C sec x tan x dx = sec x + C
| 6. 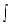 csc x cot x dx = -csc x + C csc x cot x dx = -csc x + C
|
7. 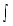 tan x dx = -ln |cos x| + C tan x dx = -ln |cos x| + C
| 8. 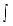 cot x dx = ln |sin x| + C cot x dx = ln |sin x| + C
|
9. 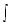 sec x dx = ln |sec x + tan x| + C sec x dx = ln |sec x + tan x| + C
| 10. 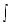 csc x dx = -ln |csc x + cot x| + C csc x dx = -ln |csc x + cot x| + C
|
11. 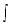 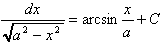
| 12. 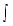 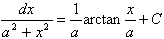
|
13. 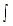 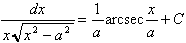
|
Integration by Substitution
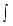 ƒ(g(x))g'(x)
dx = F(g(x)) + C
ƒ(g(x))g'(x)
dx = F(g(x)) + C
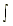 ƒ(u) du
= F(u) + C
ƒ(u) du
= F(u) + CIntegration by Parts
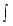 u dv = uv -
u dv = uv - 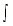 v
du
v
duDistance, Velocity, and Acceleration (on Earth)
a(t) = s''(t) = -32 ft/sec2
v(t) = s'(t) = 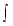
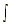
at t = 0, v0 = v(0) = (-32)(0) + C1 = C1
s(t) = 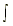
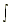
Separable Differential Equations
It is sometimes possible to separate variables and write a differential equation in the form
ƒ(y) dy + g(x) dx = 0 by integrating:
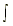 ƒ(y) dy +
ƒ(y) dy + 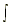 g(x)
dx = C
g(x)
dx = C
| Exercise: | Solve for 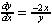
|
| 2x dx + y dy = 0 | |
x2 + 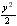 = C = C
|
Applications to Growth and Decay
Often, the rate of change or a variable y is proportional
to the variable itself.
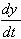 = ky = ky
| separate the variables | |
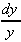 = k dt = k dt
| integrate both sides | |
| ln |y| = kt + C1 | ||
| y = Cekt | Law of Exponential Growth and Decay | |
| Exponential growth when k 0 | ||
| Exponential decay when k 0 | ||
Definition of the Definite Integral
The definite integral is the limit of the Riemann sum of ƒ on the interval [a, b]
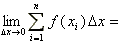
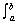 ƒ(x)
dx
ƒ(x)
dxProperties of Definite Integrals
1. 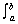
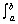
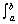
2. 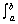
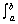
3. 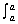
4. 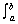
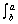
5. 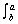
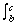
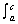
6. If ƒ(x) g(x) on [a, b],
then 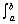
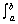
Approximations to the Definite Integral
Riemann Sums
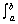
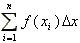
Trapezoidal Rule
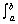
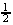
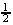
The Fundamental Theorem of Calculus
If ƒ is continuous on [a, b] and if F' = ƒ, then
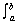 ƒ(x) dx = F(b)
- F(a)
ƒ(x) dx = F(b)
- F(a)The Second Fundamental Theorem of Calculus
If ƒ is continuous on an open interval I containing a, then for every x in the interval,
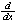
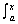 ƒ(t)
dt = ƒ(x)
ƒ(t)
dt = ƒ(x)Area Under a Curve
| If | ƒ(x)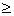 0 on [a, b] 0 on [a, b]
| A = 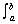 ƒ(x) dx ƒ(x) dx
|
| If | ƒ(x)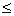 0 on [a, b] 0 on [a, b]
| A = -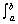 ƒ(x) dx ƒ(x) dx
|
| If | ƒ(x)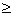 0 on [a, c] and 0 on [a, c] and
| A = 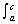 ƒ(x) dx - ƒ(x) dx - 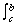 ƒ(x) dx ƒ(x) dx
|
ƒ(x)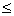 0 on [c, b] 0 on [c, b]
|
| Exercise | The area enclosed by the graphs of y = 2x2 and y = 4x + 6 is: | |
| (A) 76/3 | ||
| (B) 32/3 | ||
| (C) 80/3 | ||
| (D) 64/3 | ||
| (E) 68/3 | ||
| The answer is D. | Intersection of graphs: | 2x2 = 4x + 6 |
| 2x2 - 4x + 6 = 0 | ||
| x = -1, 3 | ||
A = 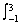 4x + 6 - 2x2 4x + 6 - 2x2
| ||
= (2x2 + 6x - 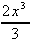 ) ) 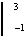
| ||
| = 18 + 18 - 18 - (2 - 6 + 2/3) | ||
| = 64/3 | ||
Average Value of a Function on an Interval
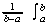 ƒ(x) dx
ƒ(x) dxVolumes of Solids with Known Cross Sections
1. For cross sections of area A(x), taken perpendicular to the x-axis:
V = 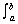
2. For cross sections of area A(y), taken perpendicular to the y-axis:
V = 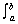
Volumes of Solids of Revolution: Disk Method
V = 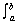 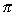 r2 dx r2 dx
| |
| Rotated about the x-axis: | V = 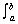 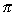 [ƒ(x)]2 dx [ƒ(x)]2 dx
|
| Rotated about the y-axis: | V = 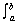 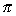 [ƒ(y)]2 dy [ƒ(y)]2 dy
|
Volumes of Solids of Revolution: Washer Method
V = 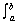 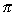 (ro2 dx - ri2 ) dx (ro2 dx - ri2 ) dx
| |
| Rotated about the x-axis: | V = 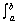 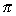 [(ƒ1(x))2 - (ƒ2(x))2] dx [(ƒ1(x))2 - (ƒ2(x))2] dx
|
| Rotated about the y-axis: | V = 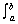 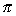 [(ƒ1(y))2 - (ƒ2(y))2] dy [(ƒ1(y))2 - (ƒ2(y))2] dy
|
| Exercise: | Find the volume of the region bounded by the y-axis, y = 4, and y = x2 |
| if it is rotated about the line y = 6. | |
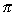 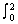 [(x2 - 6)2 - (4 - 6)2 ]dx [(x2 - 6)2 - (4 - 6)2 ]dx
| |
= 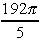 cubic units cubic units
|
Volumes of Solids of Revolution: Cylindrical Shell Method
V = 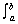 2 2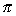 rh dr rh dr
| |
| Rotated about the x-axis: | V = 2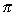 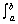 xƒ(x) dx xƒ(x) dx
|
| Rotated about the y-axis: | V = 2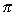 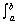 yƒ(y) dy yƒ(y) dy
|