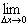
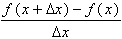
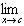
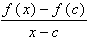



Definition
ƒ'(x) =  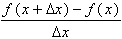
| |
ƒ'(c) = 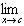 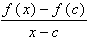
|
If ƒ is differentiable at x = c, then ƒ
is continuous at x = c.
Differentiation Rules
General and Logarithmic Differentiation Rules
1. 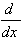 [cu] = cu' [cu] = cu'
| 2. 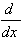 [u v] = u' v' [u v] = u' v'
| sum rule | |
3. 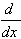 [uv] = uv' + vu' [uv] = uv' + vu'
| product rule | 4. 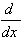 [ [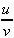 ] = ] = 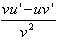
| quotient rule |
5. 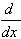 [c] = 0 [c] = 0
| 6. 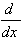 [un] = nun-1u' [un] = nun-1u'
| power rule | |
7. 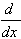 [x] = 1 [x] = 1
| 8. 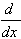 [ln u] = [ln u] = 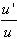
| ||
9.  [eu] = euu' [eu] = euu'
| 10. [ƒ(g(x))] = ƒ' (g(x)) g' (x) [ƒ(g(x))] = ƒ' (g(x)) g' (x)
| chain rule |
Derivatives of the Trigonometric Functions
1.  [sin u] = (cos u)u' [sin u] = (cos u)u'
| 2. 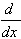 [csc u] = -(csc u cot u)u' [csc u] = -(csc u cot u)u'
|
3. 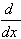 [cos u] = -(sin u)u' [cos u] = -(sin u)u'
| 4. 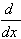 [sec u] = (sec u tan u)u' [sec u] = (sec u tan u)u'
|
5. 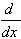 [tan u] = (sec2 u)u' [tan u] = (sec2 u)u'
| 6. 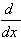 [cot u] = -(csc2 u)u' [cot u] = -(csc2 u)u'
|
Derivatives of the Inverse Trigonometric Functions
1. 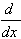 [arcsin u] = [arcsin u] = 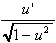
| 2. 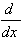 [arccsc u] = [arccsc u] = 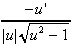
|
3. 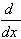 [arccos u] = [arccos u] = 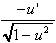
| 4. 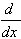 [arcsec u] = [arcsec u] = 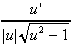
|
5. 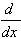 [arctan u] = [arctan u] = 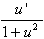
| 6. 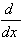 [arccot u] = [arccot u] = 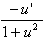
|
Implicit Differentiation
Implicit differentiation is useful in cases in which you
cannot easily solve for y as a function of x.
| Exercise: | Find 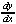 for y3 + xy - 2y - x2 = -2 for y3 + xy - 2y - x2 = -2
|
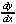 [y3 + xy - 2y - x2] = [y3 + xy - 2y - x2] = 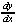 [-2] [-2]
| |
3y2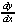 + (x + (x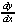 + y) - 2 + y) - 2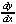 - 2x = 0 - 2x = 0
| |
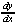 (3y2 + x - 2) = 2x - y (3y2 + x - 2) = 2x - y
| |
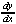 = = 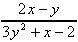
|
Higher Order Derivatives
These are successive derivatives of ƒ(x). Using prime notation, the second derivative of ƒ(x), ƒ''(x), is the derivative of ƒ'(x). The numerical notation for higher order derivatives is represented by:
The second derivative is also indicated by 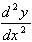
| Exercise: | Find the third derivative of y = x5. |
| y' = 5x4 | |
| y'' = 20x3 | |
| y''' = 60x2 |
Derivatives of Inverse Functions
If y = ƒ(x) and x = ƒ-1(y) are differentiable inverse functions, then their derivatives are reciprocals:
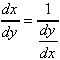
Logarithmic Differentiation
It is often advantageous to use logarithms to differentiate certain functions.
1. Take ln of both sides
2. Differentiate
3. Solve for y'
4. Substitute for y
5. Simplify
| Exercise: | Find 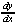 for y = for y = 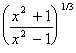
|
ln y = 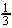 [ln(x2 + 1) - ln(x2 - 1)] [ln(x2 + 1) - ln(x2 - 1)]
| |
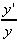 = = 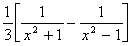
| |
y' = 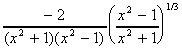
| |
y' = 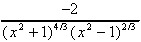
|
Mean Value Theorem
If ƒ is continuous on [a, b] and differentiable on (a, b), then there exists a number c in (a, b) such that
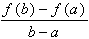
L'Hôpital's Rule
If lim ƒ(x)/g(x) is an indeterminate
of the form 0/0 or 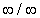
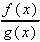 = lim
= lim 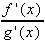
The indeterminate form 0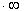
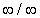
Note: L'Hôpital's Rule can be applied to the four
different indeterminate forms of 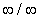
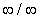
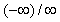
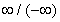
| Exercise: | What is 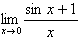 ? ?
|
| (A) 2 | |
| (B) 1 | |
| (C) 0 | |
(D) 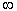
| |
| (E) The limit does not exist. | |
| The answer is B. | 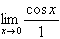 = 1 = 1
|
Tangent and Normal Lines
The derivative of a function at a point is the slope of the tangent
line. The normal line is the line that is perpendicular
to the tangent line at the point of tangency.
| Exercise: | The slope of the normal line to the curve y = 2x2 + 1 at (1, 3) is |
| (A) -1/12 | |
| (B) -1/4 | |
| (C) 1/12 | |
| (D) 1/4 | |
| (E) 4 | |
| The answer is B. | y' = 4x |
| y = 4(1) = 4 | |
| slope of normal = -1/4 |
Extreme Value Theorem
If a function ƒ(x) is continuous on a closed interval,
then ƒ(x) has both a maximum and minimum value in
the interval.
Curve Sketching
| Situation | Indicates |
| ƒ'(c) > 0 | ƒ increasing at c |
| ƒ'(c) < 0 | ƒ decreasing at c |
| ƒ'(c) = 0 | horizontal tangent at c |
| ƒ'(c) = 0, ƒ'(c-) < 0, ƒ'(c+) > 0 | relative minimum at c |
| ƒ'(c) = 0, ƒ'(c-) > 0, ƒ'(c+) < 0 | relative maximum at c |
| ƒ'(c) = 0, ƒ''(c) > 0 | relative minimum at c |
| ƒ'(c) = 0, ƒ''(c) < 0 | relative maximum at c |
| ƒ'(c) = 0, ƒ''(c) = 0 | further investigation required |
| ƒ''(c) > 0 | concave upward |
| ƒ''(c) < 0 | concave downward |
| ƒ''(c) = 0 | further investigation required |
| ƒ''(c) = 0, ƒ''(c-) < 0, ƒ''(c+) > 0 | point of inflection |
| ƒ''(c) = 0, ƒ''(c-) > 0, ƒ''(c+) < 0 | point of inflection |
| ƒ(c) exists, ƒ'(c) does not exist | possibly a vertical tangent; possibly an absolute max. or min. |
Newton's Method for Approximating Zeros of a Function
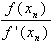
To use Newton's Method, let x1 be a
guess for one of the roots. Reiterate the function with the result
until the required accuracy is obtained.
Optimization Problems
Calculus can be used to solve practical problems requiring maximum
or minimum values.
| Exercise: | A rectangular box with a square base and no top has a volume of 500 cubic |
| inches. Find the dimensions for the box that require the least amount of | |
| material. | |
| Let V = volume, S = surface area, x = length of base, and h = height of box | |
| V = x2h = 500 | |
| S = x2 + 4xh = x2 + 4x(500/x2) = x2 + (2000/x) | |
| S' = 2x - (2000/x2) = 0 | |
| 2x3 = 2000 | |
| x = 10, h = 5 | |
| Dimensions: 10 x 10 x 5 inches | |
Rates-of-Change Problems
Distance, Velocity, and Acceleration
y = s(t) position of a particle along a line at time t
v = s'(t) instantaneous velocity (rate of change) at time t
a = v'(t) = s''(t) instantaneous acceleration
at time t
Related Rates of Change
Calculus can be used to find the rate of change of two or more
variable that are functions of time t by differentiating
with respect to t.
| Exercise: | A boy 5 feet tall walks at a rate of 3 feet/sec toward a streetlamp that is | |
| 12 feet above the ground. | ||
| a) What is the rate of change of the tip of his shadow? | ||
| b) What is the rate of change of the length of his shadow? | ||
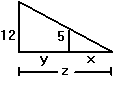 | 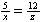
| 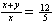 |
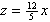
| 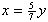 | |
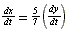
| 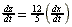 | |
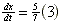
| 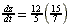 | |
b) = 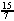 ft/sec ft/sec
| a) = 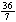 ft/sec ft/sec
| |
Note: the answers are independent of the distance from
the light.
| Exercise: | A conical tank 20 feet in diameter and 30 feet tall (with vertex down) | |
| leaks water at a rate of 5 cubic feet per hour. At what rate is the water | ||
| level dropping when the water is 15 feet deep? | ||
V = 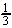 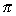 r2h r2h
|  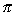 h2 h2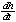
| |
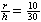
| 5 = 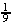 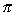 h2 h2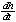
| |
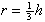
| 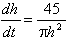 | |
V = 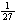 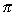 h3 h3
| 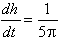 ft/hr ft/hr |
|